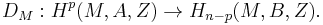Lefschetz duality
In mathematics, Lefschetz duality is a version of Poincaré duality in geometric topology, applying to a manifold with boundary. Such a formulation was introduced by Solomon Lefschetz in the 1920s, at the same time introducing relative homology, for application to the Lefschetz fixed-point theorem.[1] There are now numerous formulations of Lefschetz duality or Poincaré-Lefschetz duality, or Alexander-Lefschetz duality.
Formulations
Let M be an orientable compact manifold of dimension n, with boundary N, and let z be the fundamental class of M. Then cap product with z induces a pairing of the (co)homology groups of M and the relative (co)homology of the pair (M, N); and this gives rise to isomorphisms of Hk(M, N) with Hn - k(M), and of Hk(M, N) with Hn - k(M).[2]
Here N can in fact be empty, so Poincaré duality appears as a special case of Lefschetz duality.
There is a version for triples. Let A and B denote two subspaces of the boundary N, themselves compact orientable manifolds with common boundary Z, which is the intersection of A and B. Then there is an isomorphism
Notes
- ^ Biographical Memoirs By National Research Council Staff (1992), p. 297.
- ^ James W. Vick, Homology Theory: An Introduction to Algebraic Topology (1994), p. 171.
External links
- Hazewinkel, Michiel, ed. (2001), "Lefschetz duality", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=p073020